中考数学公式

时间：2024-11-25 13:07:36 中考我要投稿

相关推荐

中考数学公式大全

中考数学公式大全1

　　判别式

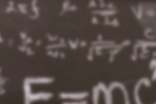
中考数学公式大全

　　b2-4ac=0 注：方程有两个相等的实根

　　b2-4ac0 注：方程有两个不等的实根

　　b2-4ac0 注：方程没有实根，有共轭复数根

　　三角函数公式

　　两角和公式

　　sin(A+B)=sinAcosB+cosAsinB sin(A-B)=sinAcosB-sinBcosA

　　cos(A+B)=cosAcosB-sinAsinB cos(A-B)=cosAcosB+sinAsinB

　　tan(A+B)=(tanA+tanB)/(1-tanAtanB) tan(A-B)=(tanA-tanB)/(1+tanAtanB)

　　ctg(A+B)=(ctgActgB-1)/(ctgB+ctgA) ctg(A-B)=(ctgActgB+1)/(ctgB-ctgA)

　　倍角公式

　　tan2A=2tanA/(1-tan2A) ctg2A=(ctg2A-1)/2ctga

　　cos2a=cos2a-sin2a=2cos2a-1=1-2sin2a

中考数学公式大全2

　　121 ①直线L和⊙O相交 d

　　② 直线L和⊙O相切 d=r

　　③ 直线L和⊙O相离 dr

　　122 切线的判定定理经过半径的外端并且垂直于这条半径的直线是圆的切线

　　123 切线的性质定理圆的切线垂直于经过切点的半径

　　124 推论1 经过圆心且垂直于切线的直线必经过切点

　　125 推论2 经过切点且垂直于切线的直线必经过圆心

　　126 切线长定理从圆外一点引圆的两条切线，它们的切线长相等，圆心和这一点的`连线平分两条切线的夹角

　　127 圆的外切四边形的两组对边的和相等

　　128 弦切角定理弦切角等于它所夹的弧对的圆周角

　　129 推论如果两个弦切角所夹的弧相等，那么这两个弦切角也相等

　　130 相交弦定理圆内的两条相交弦，被交点分成的两条线段长的积相等

　　131 推论如果弦与直径垂直相交，那么弦的一半是它分直径所成的两条线段的比例中项

　　132 切割线定理从圆外一点引圆的切线和割线，切线长是这点到割线与圆交点的两条线段长的比例中项

　　20xx中考数学公式

　　133 推论从圆外一点引圆的两条割线，这一点到每条割线与圆的交点的两条线段长的积相等

　　134 如果两个圆相切，那么切点一定在连心线上

　　135 ①两圆外离 dR+r ②两圆外切 d=R+r

　　③ 两圆相交 R-rr)

　　④ 两圆内切 d=R-r(Rr) ⑤两圆内含dr)

　　136 定理相交两圆的连心线垂直平分两圆的公共弦

　　137 定理把圆分成n(n3)：

　　⑴ 依次连结各分点所得的多边形是这个圆的内接正n边形

　　⑵ 经过各分点作圆的切线，以相邻切线的交点为顶点的多边形是这个圆的外切正n边形

　　138定理任何正多边形都有一个外接圆和一个内切圆，这两个圆是同心圆

　　139正n边形的每个内角都等于(n-2)180/n

　　140 定理正n边形的半径和边心距把正n边形分成2n个全等的直角三角形

　　141 正n边形的面积Sn=pnrn/2 p表示正n边形的周长

　　142 正三角形面积3a/4 a表示边长

　　143 如果在一个顶点周围有k个正n边形的角，由于这些角的和应为360，因此k(n-2)180/n=360化为(n-2)(k-2)=4

　　144 弧长计算公式：L=n兀R/180

　　145 扇形面积公式：S扇形=n兀R^2/360=LR/2

　　146 内公切线长= d-(R-r) 外公切线长= d-(R+r)

　　147 完全平方公式：(a+b)^2=a^2+2ab+b^2 (a-b)^2=a^2-2ab+b^2

　　148 平方差公式：(a+b)(a-b)=a^2-b^2

中考数学公式大全3

　　【两角和公式】

　　sin(A+B)=sinAcosB+cosAsinBsin(A-B)=sinAcosB-sinBcosA

　　cos(A+B)=cosAcosB-sinAsinBcos(A-B)=cosAcosB+sinAsinB

　　tan(A+B)=(tanA+tanB)/(1-tanAtanB)tan(A-B)=(tanA-tanB)/(1+tanAtanB)

　　ctg(A+B)=(ctgActgB-1)/(ctgB+ctgA)ctg(A-B)=(ctgActgB+1)/(ctgB-ctgA)

　　【三角和的三角函数】

　　sin(α+β+γ)=sinα?cosβ?cosγ+cosα?sinβ?cosγ+cosα?cosβ?sinγ-sinα?sinβ?sinγ

　　cos(α+β+γ)=cosα?cosβ?cosγ-cosα?sinβ?sinγ-sinα?cosβ?sinγ-sinα?sinβ?cosγ

　　tan(α+β+γ)=(tanα+tanβ+tanγ-tanα?tanβ?tanγ)/(1-tanα?tanβ-tanβ?tanγ-tanγ?tanα)

　　【积化和差】

　　sin(a)sin(b)=-1/2__[cos(a+b)-cos(a-b)]

　　cos(a)cos(b)=1/2__[cos(a+b)+cos(a-b)]

　　sin(a)cos(b)=1/2__[sin(a+b)+sin(a-b)]

　　cos(a)sin(b)=1/2__[sin(a+b)-sin(a-b)]

　　因式分解公式

　　公式：a^3+b^3+c^3-3abc=(a+b+c)(a^2+b^2+c^2-ab-bc-ca)

　　平方差公式：a平方-b平方=(a+b)(a-b)

　　完全平方和公式： (a+b)平方=a平方+2ab+b平方

　　完全平方差公式： (a-b)平方=a平方-2ab+b平方

　　两根式： ax^2+bx+c=a[x-(-b+√(b^2-4ac))/2a][x-(-b-√(b^2-4ac))/2a]两根式

　　立方和公式： a^3+b^3=(a+b)(a^2-ab+b^2)

　　立方差公式：a^3-b^3=(a-b)(a^2+ab+b^2)

　　完全立方公式： a^3±3a^2b+3ab^2±b^3=(a±b)^3.

　　初三数学中考排列组合公式大全

　　1.排列及计算公式

　　从n个不同元素中，任取m(m≤n)个元素按照一定的顺序排成一列，叫做从n个不同元素中取出m个元素的一个排列;从n个不同元素中取出m(m≤n)个元素的所有排列的个数，叫做从n个不同元素中取出m个元素的排列数，用符号p(n,m)表示.

　　p(n,m)=n(n-1)(n-2)……(n-m+1)= n!/(n-m)!(规定0!=1).

　　2.组合及计算公式

　　从n个不同元素中，任取m(m≤n)个元素并成一组，叫做从n个不同元素中取出m个元素的一个组合;从n个不同元素中取出m(m≤n)个元素的所有组合的`个数，叫做从n个不同元素中取出m个元素的组合数.用符号

　　c(n,m) 表示.

　　c(n,m)=p(n,m)/m!=n!/((n-m)!__m!);c(n,m)=c(n,n-m);

　　3.其他排列与组合公式

　　从n个元素中取出r个元素的循环排列数=p(n,r)/r=n!/r(n-r)!.

　　n个元素被分成k类，每类的个数分别是n1,n2,...nk这n个元素的全排列数为

　　n!/(n1!__n2!__...__nk!).

　　k类元素,每类的个数无限,从中取出m个元素的组合数为c(m+k-1,m).

　　排列(Pnm(n为下标，m为上标))

　　Pnm=n×(n-1)....(n-m+1);Pnm=n!/(n-m)!(注：!是阶乘符号);Pnn(两个n分别为上标和下标)=n!;0!=1;Pn1(n为下标1为上标)=n

　　组合(Cnm(n为下标，m为上标))

　　Cnm=Pnm/Pmm ;Cnm=n!/m!(n-m)!;Cnn(两个n分别为上标和下标) =1;Cn1(n为下标1为上标)=n;Cnm=Cnn-m

　　等比公式求和的公式

　　(1)等比数列：a(n+1)/an=q(n∈N)。

　　(2)通项公式：an=a1×q^(n-1);

　　推广式：an=am×q^(n-m);

　　①若m、n、p、q∈N，且m+n=p+q，则am__an=ap__aq;

　　②在等比数列中，依次每k项之和仍成等比数列.

　　③若m、n、q∈N，且m+n=2q，则am__an=aq^2

　　(5)"G是a、b的等比中项""G^2=ab(G≠0)".

　　(6)在等比数列中，首项a1与公比q都不为零.

【中考数学公式】相关文章：